generative-art
Table of Contents
I want to do some visualizations and generative art using Clojure. One of my goals is to make a play-through and simulate Braitenberg vehicles.
I spend time trying to do some geom, which is a really advanced lib with which you probably can do really a lot. All the examples are sort of on the edges of what you can do with the thing, so not much beginner material in the examples. Graphics and OpenGL bring together multiple high-ceiling topics: math, geometry, 3D tech, and shaders (GPU programming).
One day I will speak this language well enough so I straightforwardly know how to make a damn red triangle. Eventually, I would like to code shaders like Sebastian Lague in this crazy inspirational slime mold simulation thing.
I also tried to generate some SVG, also with geom but realized for the kind of stuff I want to do, I probably want to be more in the direction of a game engine kinda of world with update logic, instead of declaratively say the animations.
I want to make toys and game-like things. For the moment I leave both the 90s svg forms stacking approach, as well as a 3D/pixel/shader approach for another time.
I decided quil looks like it has a low floor and a high ceiling, so let's go.
Brownians
brownians #20
The Brownian world is my first generative art algorithm toy simulation world.
I came across Tyler Hobbs and decided his stuff is really cool. I started skimming probability distributions for algorithmic artists and decided I needed Gaussian Bell curves in my algorithms.
When you do biology, biochemistry and these things, almost all relationships are expressed in normal distributions a.k.a bell curves. Or as overlapping bell curves from multiple factors. Say the height of plant genotype, the count of blood cells in a sample, and the reaction times of a human.
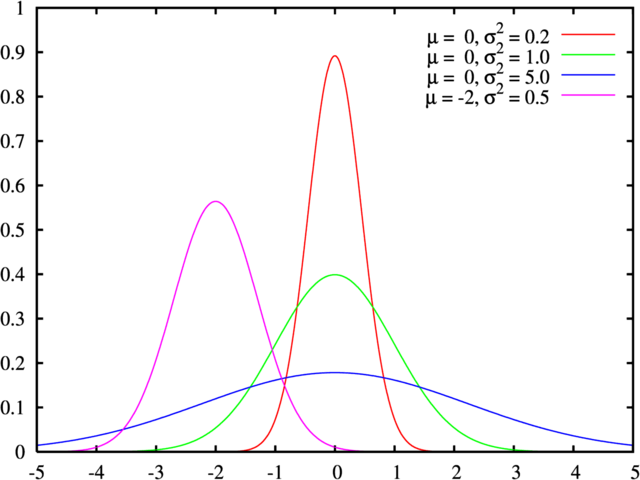
It only has 2 parameters, the mean and the standard-deviation.
With the mean, I move the curve left and right, with the std-deviation I make it taller or flatter. q/random-gaussian returns a Gaussian random number with a mean of 0 and standard deviation something - So the return values are between -1 and 1.
Quil:
(defn normal-distr [mean std-deviation] (+ mean (* std-deviation (q/random-gaussian))))
Clouds
If I spawn circles in a 2D rect using a normal distribution, I get a natural-looking cloud.
Circles in a cloud, brownians #22
spread
ChatGPT helped generate some code that made them fly away from the center.
I control it with the :spread-speed control parameter of the Brownian world.
High spread-speed setting in brownians #5
Little motions… Brownian motion!
I think I want to make the wobble around and I realize, I really want some Brownian motion algorithmic cakeness in my world.
I am not sure how accurately this is of a simulation, but making the velocity of my circles change in a normal distribution way, where 0 is the mean and they wiggle in the other directions else.1
(defn brownian-motion [entity] (let [brownian-factor (:brownian-factor (controls))] (update entity :velocity (fnil (fn [[x y]] [(+ x (* brownian-factor (q/random-gaussian))) (+ y (* brownian-factor (q/random-gaussian)))]) [0 0]))))
Well, I was very satisfied with the result. So much so that I called the whole toy world and the resulting art gallery brownians.
No spread-speed, but high brownian-factor - brownian #23
Ah brownian-factor I could have called temperature. Now the term absolute zero makes absolute sense. Brownian-factor cannot get lower than 0.
Yes, the way they are flying reminds me very much of physics/chemistry simulation gifs of these things.
Simulating infection
I added an attribute infectable? to my circles and made some of them spawn infected. Then I make some temporary lines between 2 random infected and non-infected circles.
With a normal distribution, the non-infected now too becomes infected. With full disregard for all prior art on epidemiology, there is a normal distribution in play!
I have controls infected-rate, how many circles spawn infected, :infectiousness makes it spread faster,
:infected-color and :infected-transform changes the appearance of infected ones.
Defaults with red infection circles brownian #24
Now you can look at this and see an abstract graph. This could be friends in a network with an idea spreading. A computer virus jumping between computer nodes. Or the dankest meme conquering the internet.
I played around with the controls and put some into a gallery. The code for the gallery is here.
Screencast
Probably way too lengthy. You can watch how I spent last Saturday :)
Inspirations
Footnotes:
The Wikipedia article has quite some equations.
Seems like the particle distribution follows, unsurprisingly, a normal distribution. I think my circles are quite close to this.
Most stay where they spawn and some fly off.